Die 2007 als Diplomarbeit an der TU Dresden eingereichte und 2008 im Grin-Verlag sowie 2014 im Diplomica Verlag erschienene Arbeit "Die Benford-Verteilung - Anwendung auf reale Daten der Marktforschung" von Dipl.-Math. Maja Glück beschäftigt sich ausführlich mit der Benford-Verteilung.
Einführung
Der Astronom Simon Newcomb veröffentlichte 1881 einen Artikel mit dem Titel "Note on the Frequency of Use of the Different Digits in Natural Numbers". In diesem Beitrag erläuterte er seine Beobachtung, dass die ersten Seiten von Logarithmen-Tafeln wesentlich schneller abgenutzt sind als die letzten. Er schloss daraus, dass die 1 als erste Ziffer häufiger vorkomme als die 2, die 2 häufiger als die 3 und so fort. Für seine Beobachtung gab er folgende Beschreibung an:
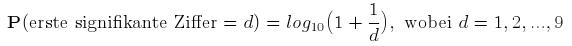
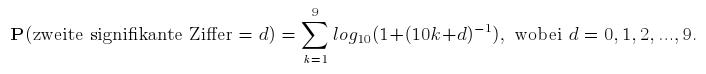
Diese Entdeckung widerspricht der allgemeinen Ansicht, dass jede Ziffer mit der gleichen Wahrscheinlichkeit - beispielsweise 1/9 für die erste Ziffer bei den Dezimalzahlen - vorkommen sollte. Lange Zeit beschäftigte sich niemand mit diesem Thema. Bekannt wurde es erst, als der Physiker Frank Benford dieselbe Beobachtung in den Logarithmen-Tafeln machte und 1938 fundiert durch eigenes Datenmaterial in dem Artikel "The law of anomalous numbers" veröffentlichte.
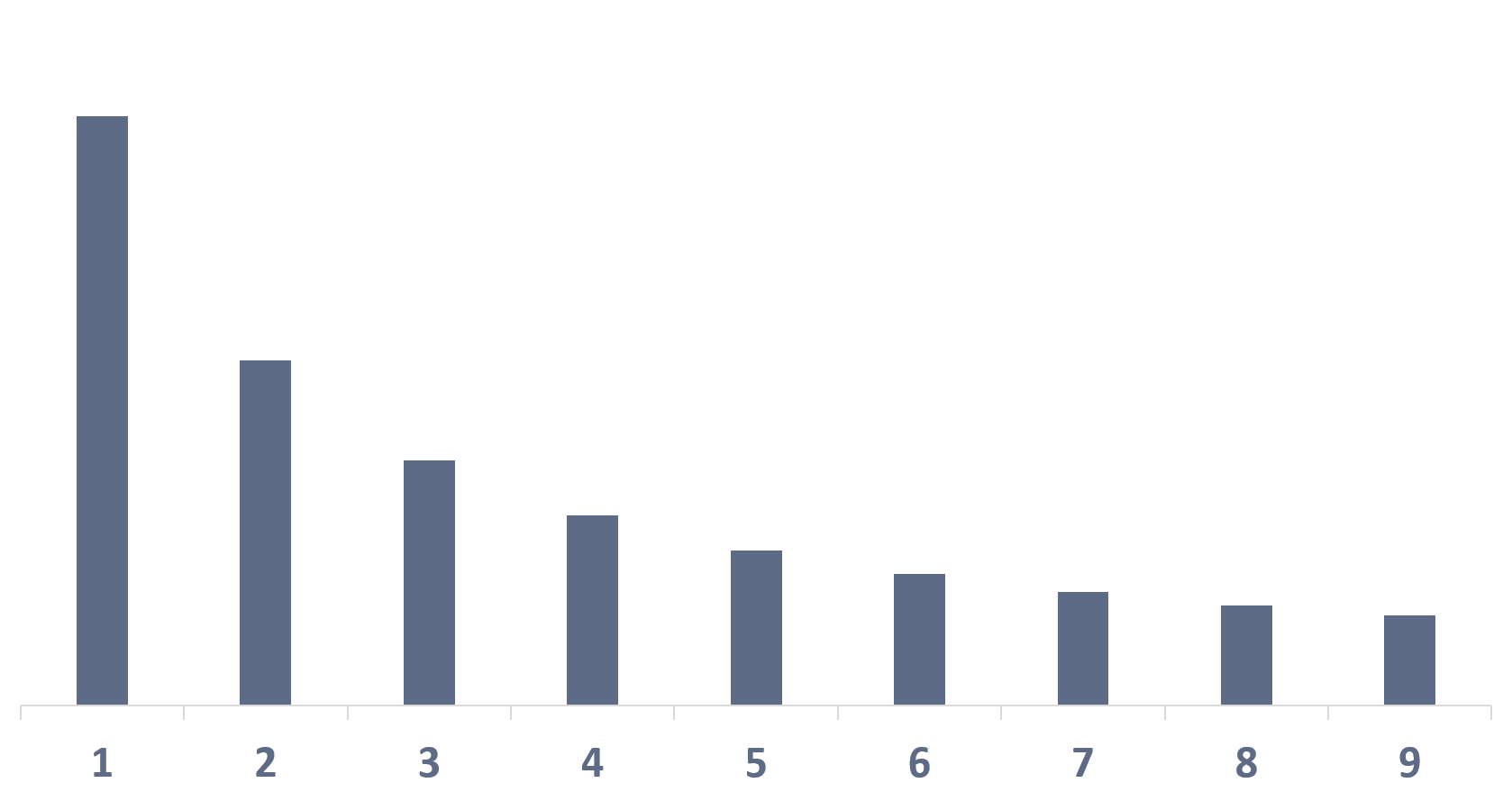
Das Gesetz ist heutzutage unter dem Namen "Benfords Gesetz" (Benford's Law) bekannt. Einige Autoren nennen es auch "Newcomb-Benford-Gesetz" (Newcomb-Benford-Law), "Gesetz der ersten Ziffern" (First Digit Law), "Gesetz der signifikanten Ziffern" (Significant Digit Law) oder "logarithmisches Gesetz" (Logarithmic Law).
Inhalt der Arbeit
Benfords Gesetz besagt kurzgefasst, dass die Anfangsziffern bestimmter Datenmengen nicht gleichverteilt sind, sondern einer logarithmischen Verteilung folgen.
Es werden ein Wahrscheinlichkeitsraum für Benfords Gesetz und Formeln für die Verteilung der ersten, zweiten und n-ten Ziffer sowie die gemeinsame Verteilung der ersten n Ziffern eingeführt. Ferner werden die besonderen Eigenschaften der Benford-Verteilung wie die Skalen- und die Baseninvarianz betrachtet. Als Hauptresultat wird ein Grenzwertsatz für signifikante Ziffern angegeben und bewiesen.
Als besondere Anwendungsmöglichkeit wird die Aufdeckung von Fälschungen bei Interviews in der Marktforschung betrachtet. Dazu werden die Prozesse der Datenerhebung beleuchtet und Ergebnisse bisheriger Studien vorgestellt. Die verschiedenen in der Marktforschung auftauchenden Datentypen werden analysiert und ihre Eignung als Prüfgrößen untersucht. Darauf aufbauend wird ein Programm zum Test auf die Benford-Verteilung vorgestellt und eine mögliche Testfrage auf Tauglichkeit untersucht.
Alle mathematischen Resultate sind in dieser Diplomverteidigung (PDF-Datei) zusammengefasst.
Weitere Informationen
Die Diplomarbeit entstand an der Technischen Universität Dresden in der Fachrichtung Mathematik am Institut für Mathematische Stochastik unter der Betreuung von Prof. Dr. rer. nat. habil. Volker N. und Dr. rer. nat. Hans-Otfried Müller. Sie wurde am 14. Februar 2007 eingereicht.
Aus dem Gutachten von Prof. Dr. Nollau:
"Die vorliegende Arbeit stellt die bekannten Resultate, deren Formulierung mathematisch sehr anspruchsvoll ist, in übersichtlicher
und konsequenter Weise dar, zumal dieser Verteilungstyp in der Standard-Literatur der Stochastik de facto nicht behandelt wird."
Bestellmöglichkeiten
Die Arbeit ist 2008 im Grin-Verlag und 2014 im Diplomica-Verlag erschienen.



